今回は、
「二次関数」
の分野について振り返っていきます。
非常に大切な分野です。
ここを理解することで、
関数や文字に強くなっていけるので、
しっかりと確認しておきましょう。
概要
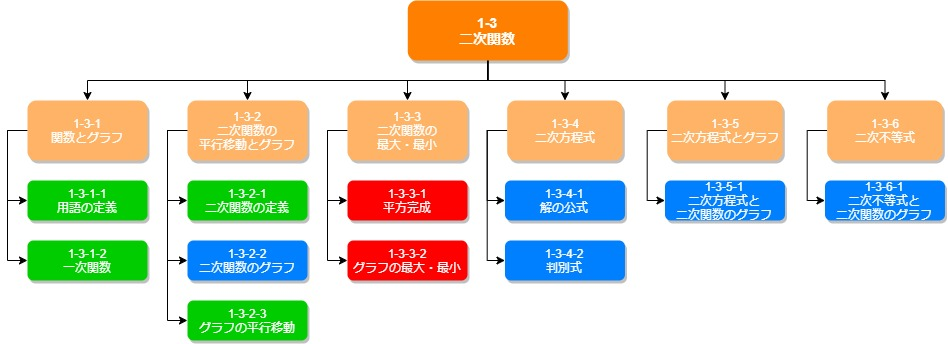
1-3-1 関数とグラフでは、
関数という定義について勉強します。
y=f(x)とは何を表しているのか、
「xが決まる事によって、yが決まる」、
という基本的な概念を勉強します。
最も基本的なところですが、
この部分を正しく理解し、
落とし込めていない人はたくさんいます。
yがxに依存しているというイメージを、
しっかりと構築しておきましょう。
また、
合わせて一次関数も学びますが、
しっかりと図を書くことを、
ここから確認しておきましょう。
正しく図示する力は、
必ず必要になってくるところなので、
初歩の初歩の段階から、
意識しておくことが大切です。
1-3-2 二次関数の平行移動とグラフでは、
二次関数の基本と平行移動を勉強します。
二次関数のグラフは次項の平方完成で勉強すればいいので、
ここではしっかり平行移動の考え方を確認しておきましょう。
平行移動の考え方も非常に大切です。
1-3-3 二次関数の最大・最小は、
非常に重要な項目です。
しっかりと演習を重ねて、
理解を深めておきましょう。
平方完成という二次関数で最も重要な考え方に加え、
場合分けという数学において非常に重要な考え方も、
勉強する事ができる項目なので、
入念に勉強しておきましょう。
平方完成を使いこなして、
正しく二次関数を図示できるようになること、
二次関数のグラフを正しく理解し使いこなせるようになること、
がこの項目の課題です。
1-3-4 二次方程式、
1-3-5 二次方程式とグラフ、
1-3-6 二次不等式では、
二次方程式や二次不等式の基本的な解法を勉強します。
1-3-3で正しく二次関数を図示し、
理解することができるようになっていれば、
何も考えなくても、
二次方程式と二次不等式を解いていくことができます。
この項目を学習しながら、
さらに二次関数のグラフの見方を勉強していきましょう。
この分野から、
本格的に数学の問題って感じになってきます。
いつも言っていることですが、
x切片、y切片や傾き、
一般型、標準型や因数分解型といった、
専門用語をしっかり押さえておきましょう。
用語を知っているだけ、
見える世界は全然違います。
また、
学校の授業などでは、
点数を取るための解き方やテクニックを教えてきます。
本当に全く意味がありません。
関数の問題で大切なのは、
正しく図示する力、
正しく場合分けする力、
それだけです。
逆にこれができていないと高みには行けません。
点数が取れているかが重要なのではありません。
しっかり理解できているかが合否を決めます。
基本を大切に勉強を進めて下さい。
考察
1-3-1 関数とグラフ
1-3-1-1 用語の定義
定義域・値域、x切片・y切片・傾き、象限など、
しっかり単語を抑えておきましょう。
1-3-1-2 一次関数
一次関数 ⇒ グラフ、
グラフ ⇒ 一次関数、
双方向を使いこなせるように、
しっかりと理解しておきましょう。
1-3-2 二次関数の平行移動とグラフ
1-3-2-1 二次関数の定義
1-3-2-2 二次関数のグラフ
一般型・標準型・因数分解型、
それぞれがどのように表され、
何を知りたい時に用いる形なのかをしっかり理解し、
グラフをしっかり描けるようにしてきましょう。
1-3-2-3 グラフの平行移動
x方向にaだけ平行移動する時は、
「x → x-a」に置き換えるという平行移動の基本を抑えておきましょう。
1-3-3 二次関数の最大・最小
1-3-3-1 平方完成
平方完成は重要な考え方なので、
しっかり覚えておきましょう。
1-3-3-2 グラフの最大・最小
ここでは、
場合分けが重要になってきます。
定義域がどのように設定されている時に、
どのように場合分けしていくのかをしっかり理解していないと、
正しく解くことはできません。
問題の全体像を把握して、
どのように場合分けをしていくのかをまず思い浮かべてから、
解答を作っていくことが大切です。
概要でも書きましたが、
授業で習うような、
こういう時はこうする的なテクニックを絶対使わない方がいいです。
しっかり理解して、
問題全体を俯瞰視する力、
そして場合分けしていく力を、
しっかりとここで身に付けてください。
必ず役に立ちます。
1-3-4 二次方程式
1-3-4-1 解の公式
解の公式は、少し複雑ですがしっかり覚えておきましょう。
1次の係数が偶数の場合の解の公式などもありますが、余裕があれば押さえておきましょう。
1-3-4-2 判別式
判別式も、
標準型のグラフを正しく描くことができれば、
全く覚える必要のないものです。
こちらも早く問題を解くためのテクニックであることを踏まえた上で、
利用するようにしましょう。
大切なのは、
正しくグラフを描いて、
グラフの意味を理解することです。
1-3-5 二次方程式とグラフ
1-3-5-1 二次方程式と二次関数のグラフ
二次方程式は、
二次関数のグラフのx切片を表しています。
しっかりとグラフの意味を理解できていれば、
簡単に想像がつくはずです。
ここを通して、
グラフの見方を改めて確認しておきましょう。
1-3-6 二次不等式とグラフ
1-3-6-1 二次不等式と二次関数のグラフ
こちらもグラフが書ければ問題ありません。
グラフを描いたうえで、
x軸より上にあるのはどこですか?
x軸より下にあるのはどこですか?
っていうのを聞いているだけです。
どのように解答していくのか、
簡単に問題を通して見直してきましょう。
まとめ
全体を通して言いたいことは、
関数の問題で大切なのはグラフです。
正しくグラフが書ければ、
問題は解いていくことができます。
これは二次関数に限らず、
数Ⅱの微積や三角関数でも同様です。
むしろ難しい問題の方が、
正確に図示していくことが求められます。
図を書かなくても解ける問題でも、
しっかり図示する癖をつけて、
正しく図を書けるように訓練していきましょう。
そして、
専門用語や定義は非常に大切です。
たくさんの言葉を学んで、
数学の視野を広げていきましょう。
今回も最後まで読んで頂きありがとうございました。
今後も宜しくお願い致します。
また、
分かりやすかった、もっとこうしてほしい、
こういう所はどうしていますか、
といったご意見・ご要望があれば、
問い合わせリンクやTwitterの方からコメント頂けると嬉しいです。
宜しくお願い致します。
P.S.
何度も書きましたが、
学校で習うような、
点数を取るためのテクニックは本当に無駄です。
特に高いレベルを目指すのであれば。
テクニックというのは、
短期的に得点を上げるために使うものでしかありません。
点数の悪い生徒がいっぱい出てきたら面目が保てないから、
自分たちのプライドのために教師たちが教えるものです。
短期的にしか物事をとらえられない人が使うものです。
行きたい大学が、
目標があるのであれば、
長期的に大きな成長をしたいのであれば、
小手先のテクニックは使わずに、
問題の本質を理解していくようにしましょう。









コメントを残す