830の数学_A_1_場合の数

今回は、「場合の数」を振り返っていきます。
確率の基礎となる範囲なので、しっかり学習していきましょう。

概要
考察
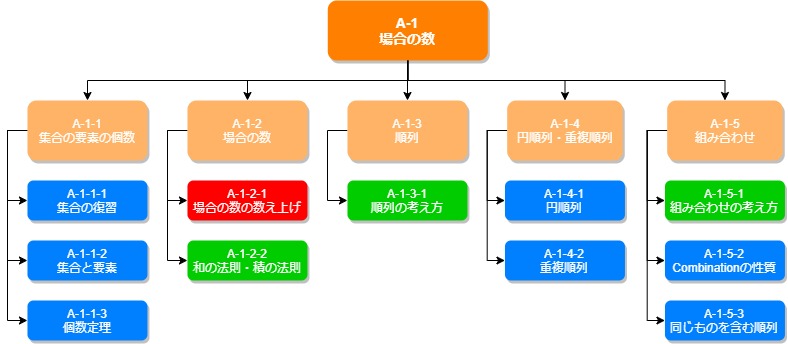
- A-1-1 集合の要素の個数
  - A-1-1-1 集合の復習
  - A-1-1-2 集合と要素
  - A-1-1-3 個数定理
- A-1-2 場合の数
  - A-1-2-1 場合の数の数え上げ
  - A-1-2-2 和の法則・積の法則
- A-1-3 順列
  - A-1-3-1 順列の考え方
- A-1-4 円順列・重複順列
  - A-1-4-1 円順列
  - A-1-4-2 重複順列
- A-1-5 組み合わせ
  - A-1-5-1 組み合わせの考え方
  - A-1-5-2 Combinationの性質
  - A-1-5-3 同じものを含む順列

概要

場合の数は、順列と組み合わせの二つからなるという事をしっかり意識しておきましょう。解いていく問題が、順列の問題なのか、組み合わせの問題なのかを把握することから場合の数の問題は始まります。
それぞれの根底になる考え方が数え上げです。数え上げでは、場合の数をどのようにグループ分けして数え上げていくのか、全体を俯瞰視する能力が必要になってきます。数学Ⅰの分野で学んできた、「場合分け」を使いこなして頭の中を整理していけるといいでしょう。

A-1-1 集合の要素の個数では、集合と要素の考え方を確認していきます。集合の基本的な考え方を、記号を使った表現方法を見直してから、集合の具体的な要素について考えていきます。この項で使うベン図は非常に役立つ図なので、使い方・見方を確認しておきましょう。

A-1-2 場合の数の数え上げでは、樹形図の使い方を学んでいきます。どんどん場合の数を枝分かれさせながら分類していくことで数え上げていく手法です。この手法は、トップダウン的に思考を整理するのに非常に役立つので、必ず学んでおくべきです。しっかり使いこなせるように落とし込んでおきましょう。和の法則・積の法則では、場合の数を数え上げる際、どのような時に足し算を使い、どのような時に掛け算を使うのかを表しています。樹形図を見れば一目瞭然なのですが、樹形図を書かなくても想像できるようにたくさん演習をこなして使い慣れておくといいでしょう。

A-1-3 順列では、Permutation(nPr)の使い方から、実践的な順列の問題まで勉強していきます。ここも初めは樹形図を使いながら整理していくことになりますが、慣れてくれば頭の中でイメージできるようになっていきます。初めは大変ですが、頑張って演習を重ねて慣れていきましょう。
また、数字の並べ替えなどを考える際は、0や重複に十分な注意が必要です。さらに、2,3,4,5,6,8,9の倍数の性質なども把握しておかないと解答していけないので、ここで倍数の性質をしっかり確認しておきましょう。

A-1-4 円順列と重複順列では、順列の問題の中でも特殊な2つの問題を取り上げています。それぞれしっかり解き方を覚えるとともに、円順列や重複順列といった問題の名称もしっかり覚えておくといいでしょう。問題の名称を知ることで勉強を効率よくしていくことができます。名称を知っていれば「円順列を間違ちゃったから円順列を復習しておこう」と考えられますが、名称を知らなければ「順列を間違ちゃったから順列を復習しておこう」となってしまいます。どちらの勉強法が効率がいいのかは一目瞭然です。こういった観点から、用語というのは非常に大切なので、解き方だけではなく、問題の名称までしっかり押さえておくといいでしょう。

A-1-5 組み合わせでは、Combination(nCr)の使い方から、実践的な問題まで勉強していきます。様々な問題があるので、正直説明は難しいです。演習あるのみと言ってしまえばそれまでなのですが、830は組み分け問題・多角形問題・塗分け問題・カード選択問題など、できる限り問題に名前をつけていくように心掛けていました。上記したように、できる限り問題を細分化して、ここが苦手だっていう領域を小さくすることができれば、勉強効率を上げていけると考えています。数学で学んだ場合分けを、勉強全体において活用して、トップダウン的に数学を分類していけると理解が進むのではないでしょうか。その一つの手法として、毎回のブログで載せているように、図を用いて視覚化しながら全体把握を進めていけるといいのではないでしょうか。

考察

A-1-1 集合の要素の個数

A-1-1-1 集合の復習

1-2 集合と命題を見直しましょう。

A-1-1-2 集合と要素

集合の要素を表す∈という記号や、集合の要素数を表すn(A)といった表現方法を勉強しておきましょう。

A-1-1-3 個数定理

ベン図の見方を勉強します。しっかりと考えらればわざわざ項目分けして勉強するほどの内容でもないのですが、ベン図の重なり部分に含まれる要素数をどのように取り扱っていくのかを確認しておきましょう。

A-1-2 場合の数

A-1-2-1 場合の数と数え上げ

樹形図を勉強していきます。数え上げの中で、文字の重複や「0」の取り扱いなど、ポイントになるところがいくつかあるので、特殊な場合にであったらその都度しっかり理解していくように心掛けましょう。

A-1-2-2 和の法則と積の法則

場合の数を数える際に、どのような時に足し算を使い、どのような時に掛け算を使うのかというのが、和の法則と積の法則になります。慣れればすぐイメージできるようになるのですが、慣れるまでは樹形図などを利用してその都度しっかり考えていくといいでしょう。

A-1-3 順列

A-1-3-1 順列の考え方

順列とは並べ替え問題です。その中で、nPrという表現を使ったりするので、確認しておきましょう。使わなくても考えていくことはできますが、使った方が便利だから開発された表現です。面倒くさがらずにに使いこなしていきましょう。
数字の並べ替え問題や人の並べ替え問題、文字の並べ替え問題や塗分け問題など、さまざまな種類の問題がありますが、自分なりに分類していきながら整理していけるといいでしょう。

A-1-4 円順列・重複順列

A-1-4-1 円順列

順列問題の中で特殊な考え方をするものの一つとして円順列が挙げられます。円順列では、一つのものを固定して、それ以外をどのように並べ替えるかを考えていくことになります。6人の円卓席の並べ替えるのであれば、一人を固定して、その一人から他の5人がどのような順番で見えるのかを考え、5人の順列を考えていく問題に変わります。この円順列の考え方の基本である、一つを固定するという考え方を抑えておきましょう。
さらに、円順列に反転を組み入れた数珠順列という問題もあるので合わせて確認しておけるといいでしょう。

A-1-4-2 重複順列

もうひとつ特殊な順列として重複順列が挙げられています。こちらは指数を用いて表現していくという点で少し特殊は形にはなっていますが、難しくはありません。簡単に確認しておきましょう。

A-1-5 組み合わせ

A-1-5-1 組み合わせの考え方

組み合わせとは、順列から概念という概念を取り払った問題です。nCrという表現を使うので覚えておきましょう。組み合わせの問題も順列と同じように、組み分け問題・多角形問題・塗分け問題・カード選択問題などのように分類をしながら学習していけるといいでしょう。

A-1-5-2 Combinationの性質

「nCr = nCn-r」
「nCr = n-1Cr-1 + n-1Cr」
といった性質を確認しておきましょう。
いずれも考えればわかるものなので、覚える必要はありませんが、理解はしておきましょう。また、nCrのnPrを用いた書き換えも大切なのでしっかり確認しておきましょう。

A-1-5-2 同じものを含む順列

こちらは順列と組み合わせの融合問題です。考え方を知っているかどうかで、知っていれば得に難しい問題でもないので、しっかりここで確認しておきましょう。

まとめ

今回は、「場合の数」の分野を振り返りました。

問題の種類が多く、慣れるまで非常に大変かと思います。しかし、覚える事がめちゃくちゃ多いという訳ではありません。全ての問題において、順列・組み合わせの基本的なところは共通しています。しっかり基本を抑えておけば、慣れるのも早くなるのではないでしょうか。

特にこの分野で大切なのは、問題の分類です。様々な種類の問題が出てきますが、それらをなんとなくこなしているといつまで経っても解けるようにはなりません。しっかり問題ごとに名称を付けて、この問題は解ける、この問題は苦手だという風に認識していくことが大切です。そのために、円順列や重複順列といった問題の名称まで覚えていくことは大切ですし、名称がない問題も組み分け問題や数字の並べ替え問題というように名前をつけていくことが大切です。

分野全体を俯瞰視して、自分はどこまで理解できるのか、どういう問題が苦手なのか、しっかりマップを作っていくことが大切なのではないでしょうか。最終的にはそのマップを数学全体に、受験勉強の範囲全体に広げていくことができれば、自分の得意・不得意をしっかりと認識できて、効率よく勉強を進めていくことができるのではないでしょうか。

概要