830の数学_A_2_確率

今回は数学Aの二回目として、
「確率」
の分野を振り返っていきます。
この分野は、難しい問題ですが、頻出です。高得点を取るためにはしっかり理解を深めていかないといけないところ。微積などは難しいイメージが強いかもしれませんが、830的に柔軟に頭を使わないといけないのは確率の分野です。しっかり理解して、どんな問題にも対応できるようにしておきましょう。

チャート式基礎からの数学1＋A増補改訂版 価格：2101円（税込、送料無料) (2020/3/12時点)

目次

• 概要
• 考察
  • A-2-1 事象と確率
    • A-2-1-1確率の定義
  • A-2-2 確率の基本性質
    • A-2-2-1 基本的性質
    • A-2-2-2 積事象・和事象
    • A-2-2-3 排反事象
    • A-2-2-4 余事象の確率
  • A-2-3 独立な試行・反復試行の確率
    • A-2-3-1 独立な試行の確率
    • A-2-3-2 反復試行の確率
  • A-2-4 条件付き確率
    • A-2-4-1 条件付き確率
• まとめ

概要

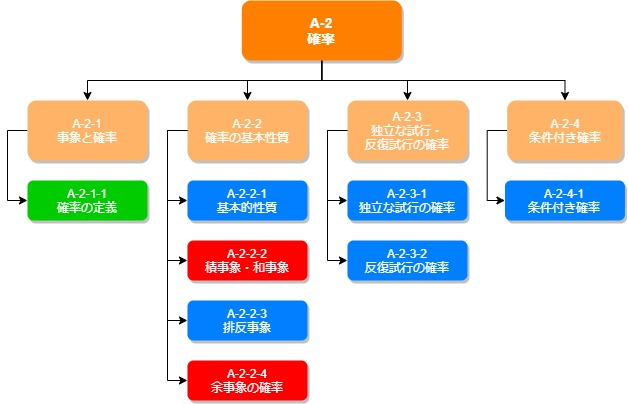
この分野では、確率について学んでいきます。

A-2-1 事象と確率では、確率の基本を確認します。確率の基本は、「(確率)=(条件を満たす事象)/(総事象)」です。A-1 場合の数の分野で学んだ考え方を用いて、総事象・条件を満たす事象の数をそれぞれすることで、確率を計算することができます。これだけを考えれば解答していくことができるので、迷った時はこの原点に返って問題を見直してみるといいでしょう。

A-2-2 確率の基本性質では、どのような時に掛け算を使うのか、足し算を使うのかをしっかり押さえておくことが大切です。A-1-2-2で勉強した和の法則・積の法則に似た部分なので、合わせて勉強できるとすばらしいでしょう。ここも慣れるまではパッと思いつかないかもしれませんが、考えなくてもなんとなくイメージできるよくらいまで理解を深めておけるといいでしょう。「慣れる」ことが大切です。たくさんの問題を解いていくことが重要でしょう。

A-2-3 独立な試行の確率・反復試行の確率、A-2-4 条件付き確率は確率の問題の中でも特殊なものを勉強する項となっています。それぞれ個別に項目を取って解法を勉強していきますが、根本にある考え方はここまでで学んできた確率の基本です。基本をしっかり押さえた上で、これらの問題の解法も基本にリンクさせながら覚えていけるといいのではないでしょうか。確かにこれらの問題は頻出ですが、間違っても基本を飛ばして特殊な解法だけを覚えないようにしましょう。直近的には問題を解けるようになるかもしれませんが、応用問題には対応できなくなってしまうので、あくまで基本を大切に勉強していけるように心掛けましょう。

考察

A-2-1 事象と確率

A-2-1-1確率の定義

確率の最も基本的な考え方は、場合の数を考慮した上で、
(確率)=(条件を満たす事象数)/(総事象数)
となっています。
応用問題で悩んだ時こそ、この基本に立ち返る事が重要です。成長が止まった時、どうしても理解ができない時は、往々にして基本的なところがネックになっています。ここの考え方は本当に当然な内容ですが、しっかり確認しておきましょう。

A-2-2 確率の基本性質

A-2-2-1 基本的性質

ここで学ぶ確率の基本性質は、空事象の確率はP(∅)=0、全事象の確率はP(U)=0、ある事象の確率は0<P(A)<1であることです。基本の基本ですが、しっかり押さえておきましょう。

A-2-2-2 積事象・和事象

ここでは、二つの確率を足すのか、掛けるのかを判断する勉強を行います。慣れるまでは難しい所ですが、演習を重ねて少しずつ理解を進めていきましょう。これを用いて様々な事象の確率を考えていくことができます。ベン図を用いると、確率を掛け合わせるのか、足し合わせるのか、はたまた足し合わせた上である確率を引かないといけないのかなどを視覚的に理解していくことができます。ここまでで学んできたものをどのように活用していくのかも意識しながら勉強を進めていけるといいでしょう。

A-2-2-3 排反事象

「排反」とは、同時に起こらない事象のことを指します。例えば、一つのサイコロを振った時に、1が出る事象と2が出る事象は同時に起こりえず、排反な試行と考える事ができます。ベン図で言うと、全く重なりを持たない二つの事象と表されます。「排反」かどうかの判断は問題を解く上で非常に大切なので、しっかり押さえておきましょう。

A-2-2-4 余事象の確率

余事象とは、ある事象以外のすべての事象のことを指します。例えば、1つのサイコロを振って1が出る事象の余事象は、1つのサイコロを振って2~6が出る事象となります。ある事象の確率を考える時に、余事象の確率を考えてから、全事象の確率から余事象の確率を引いた方が簡単な時に、この余事象を利用していくことになります。この考え方は、1-2-3-2 背理法の考え方とよく似ています。合わせて確認しておくといいでしょう。

A-2-3 独立な試行・反復試行の確率

A-2-3-1 独立な試行の確率

独立な試行とは、その名の通り、お互いに全く関連性を持たない試行のことを表します。1つのサイコロを振って、1つのコインを投げる時、これらはお互いに影響を及ぼし合わない試行なので、独立な試行と考える事ができます。このような試行を考える時、サイコロの目が1になって、コインが表を向く確率を計算するためには、それぞれの確率を掛け合わせていきます。難しい考え方ではないですが、問題が出てきた時に、「あー、独立試行の問題だな」って思う事ができれば、試験中でも安心する事ができるので、しっかり問題の名前も合わせて勉強しておけるといいでしょう。

A-2-3-2 反復試行の確率

ここでは、1つのサイコロを振る試行を何回も繰り返すといったように、同じ試行を繰り返すといった状況を考えます。nCrを用いて考える特殊な問題ですが、しっかり意味も含めて理解しておきましょう。サイコロを何度も投げる問題や、道順を考える問題など、どのような問題があるのかも含めて押さえておきましょう。

A-2-4 条件付き確率

A-2-4-1 条件付き確率の考え方

条件付き確率は、表現がややこしく、理解が難しい所です。しかしこの問題も、A-2-1-1 確率の定義に照らし合わせて考えると理解しやすくなると思います。基本を大切にしてこの考え方も理解するといいでしょう。

まとめ

今回は、A-2 確率の分野を振り返っていきました。独立試行の確率や反復試行の確率、条件付き確率など、それぞれの問題についてあたかも特殊な考え方をするかのように説明する先生や教材が多いように感じます。しかし、それぞれを考える上で大切になるのは基本的なところで 、積事象や和事象の確率をどのように考えるのかや確率の定義などです。小手先のテクニックのように問題の解き方を覚えていくのではなくて、基本とリンクさせた上で、なぜそのような考え方をしていくのかまでしっかり理解しておかないと、応用問題に対応していくことができません。しっかり考え方を理解した上で、演習を重ねて素早く解答していけるように、様々な問題に対応していけるように勉強を進めていきましょう。

今回も最後まで読んで頂きありがとうございました。
今後も宜しくお願い致します。

チャート式基礎からの数学1＋A増補改訂版 価格：2101円（税込、送料無料) (2020/3/12時点)