830の数学_A_3_図形の性質

今回は、「図形の性質」を振り返っていきます。
覚える事も大ですし、証明問題も多いので、かなり厄介な範囲ではありますが、しっかり確認していきましょう。

チャート式基礎からの数学1＋A増補改訂版 価格：2101円（税込、送料無料) (2020/3/13時点)

目次

• 概要
• 考察
  • A-3-1 三角形の辺の比、五心
  • A-3-2 チェバの定理、メネラウスの定理
  • A-3-3 三角形の辺と角
  • A-3-4 円に内接する四角形
  • A-3-5 円と直線、2つの円の位置関係
  • A-3-6 作図
  • A-3-7 空間図形
• まとめ

概要

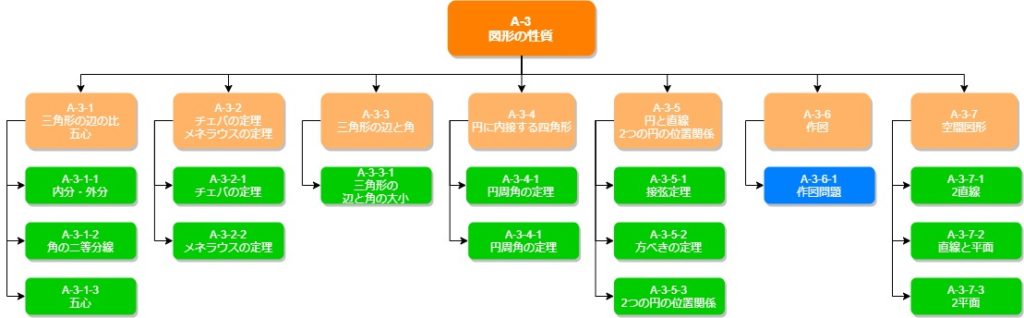
上の図を見てもらうとわかる通り、ほとんどが緑色です。どこの部分、それぞれ独立して問題となっていくので、どこが欠けても失点につながってしまいます。全て基本的な定理などを表していて、覚えないとどうしようもない部分です。覚える事が非常に多くややこしいですが頑張りましょう。
また、A-3 図形の性質では証明問題がたくさん出てくるので、しっかり証明の書き方を学んでいきましょう。∵や∴といった記号や、Q.E.D.などといった言葉も使いこなせると見栄えのいい解答を作っていけるでしょう。

A-3-1~A-3-5までは定理を覚えていくしかありません。大変ですが、問題を解きながら覚えていきましょう。単に定理を読み込むだけではなくて、実際に問題の中で使っていくことが効率よく身に付けていくことができます。何事も実践が大切です。どんどん演習をこなして、覚えていきましょう。

A-3-6 作図問題は入試問題出題されることはまずありませんが、しっかり押さえておくといいでしょう。図形問題では的確に図を描けないと理解が難しくなってしまう場面も多々見られます。きちんとした図を描けるようにするためにも作図問題もしっかりと理解しておきましょう。

A-3-7 空間図形ではねじれの位置や直線と平面の関係など、空間ならではの考え方を学んでいきます。基本的に空間の問題は平面に落とし込んでいくことが最も大切なポイントになります。三次元を考えるのは人間の頭では難しいので、どの平面に注目すれば問題に対応することができるのか、ポイントとなる平面を見つけ出すことが最も大切な作業になります。このことを念頭に置いたうえで、ねじれの位置や2平面の交わりなど、二次元に落とし込めないような問題の考え方を確認しておくといいでしょう。

簡単に説明はしましたが、覚える事が非常に多い範囲です。しかし、逆に言えば、覚えてしまえば簡単に解いていくことができる分野でもあります。苦手意識を持たず向かっていきましょう。合わせて証明問題の耐性もつけていくことが大切です。難易度の高い問題では、証明問題で大きく差がついてきます。命題を証明するためには、何と何と何が必要なのか、それぞれをどのように説明していくとわかりやすいのか、解答の全体像を思い浮かべられるように意識して勉強していきましょう。

考察

A-3-1 三角形の辺の比、五心

A-3-1-1 内分・外分

線分の内分・外分の考え方を確認しておきましょう。

A-3-1-2 角の二等分線

角の二等分線は内分・外分に密接に関係します。内角・外角の二等分線と内分・外分の関係を確認しておきましょう。

A-3-1-3 五心

五心とは、外心・垂心・内心・重心・傍心から成ります。
外心は、垂直二等分線の交点で、外接円の中心です。
垂心は、各頂点から下ろした垂線の交点を表します。
内心は、角の二等分線の交点で、内接円の中心です。
重心は、中線の交点を表します。中線定理と合わせて確認しておきましょう。
傍心は、1つの内角と2つの外角の二等分線の交点です。
それぞれ、性質や頻出の問題形式と合わせて確認しておきましょう。

A-3-2 チェバの定理、メネラウスの定理

A-3-2-1 チェバの定理

チェバの定理・メネラウスの定理は、その逆を用いることによって、3直線が1点で交わる事を証明する問題が頻出です。どのような解答を作っていくのかしっかり確認しておきましょう。しかしながら、入試問題で出題されることはまずないので、証明の書き方を学ぶ一例として捉えておけばいいでしょう。

A-3-2-2 メネラウスの定理

A-3-3 三角形の辺と角

A-3-3-1 三角形の辺と角の大小

三角形の内角の大小が、対辺の大小と一致するというのがポイントになります。結構直観的にイメージしやすいので、簡単に流してしまって、問題に直面した時に、「これでよかったっけ？」ってなってしま否ところです。しっかり押さえておきましょう。

A-3-4 円に内接する四角形

A-3-4-1 円周角の定理

ある円の中において同じ円弧を持つ扇型の中心角は常に等しいという定理です。 また、同じ円弧を持つ扇形を考える時、扇形の中心が円の中心にある時、その角は扇形の中心が演習にある時の2倍になるというのも円周角の定理の一つなので、しっかり覚えておきましょう。こちらは見落としがちです。 言葉にするとわかりにくいですが、かなり有名な考え方です。問題の中でも使いこなせるようにしておきましょう。また、ここも証明問題と合わせて確認しておくといいでしょう。

A-3-4-2 円に内接する四角形

円に内接する四角形の対角の和は180°になるというのが円に内接する四角形の性質です。証明問題と合わせて確認しておきましょう。

A-3-5 円と直線、2つの円の位置関係

A-3-5-1 接弦定理

円に内接する三角形の内角と、接線と三角形が作る角の関係性を表した定理になります。知らないと説くことができないものなのでしっかり確認しておきましょう。この定理も見落としがちなので注意しましょう。

A-3-5-2 方べきの定理

方べきの定理は、2直線の交点が円の中にあるパターンと円の外にあるパターン、2直線の内一方が接線であるパターンなど、様々なケースがあるのでそれぞれに対応できるようにしておきましょう。

A-3-5-3 2つの円の位置関係

2つの円の位置関係には、外部にある・外接する・2点で交わる・内接する・内部にあるの5パターンが考えられます。それぞれの中心間の距離と半径の関係、共通接線がどのように引けるのかなど抑えておきましょう。

A-3-6 作図

A-3-6-1 作図問題

作図問題は、コンパスをどのように使うのかを勉強する問題です。試験ではコンパスは使えないので、出題されません。それでも、しっかり視覚的に勉強しておくことで、ここまでで覚えてきた内容も身につきやすくなるので、甘く考えずに勉強しておくことをおススメしています。

A-3-7 空間図形

A-3-7-1 2直線

空間の中で2直線の関係は、1点で交わる・平行・ねじれの3つに分けられます。また、1点で交わる時、2直線から作られる角度の内小さい方を2直線のなす角と言います。

A-3-7-2 直線と平面

空間の中での直線と平面の関係は、直線が平面に含まれる・1点で交わる・平行の3つに分けられます。直線と平面が垂直である事をどのように証明するのかまで確認しておきましょう。

A-3-7-3 2平面

空間の中での2平面の関係は、交わる・平行の2つに分けられます。また、交わる時、交線上の一点から各平面上に交線に対して垂直に引いた2直線のなす角を、2平面のなす角と言います。

まとめ

今回は、A-3 図形の性質を見直してきました。繰り返しで申し訳ありませんが、非常に覚える事が多い。どれも定理なので、理解するというよりも、覚えるしかないというのが厄介なところです。演習をこなして、問題の中でどのように使っていくのかとリンクさせることで覚えやすくなっていくと思います。頑張っていきましょう。

また、この分野では様々な証明問題に触れる事ができます。証明問題に苦手意識を持つ受験生は多いですが、こういった所から証明問題が合否を分けるという事を意識しながら大切取り組んでいきましょう。次回のA-4 整数の性質ではさらに難しい証明問題がたくさん出てきます。その準備としてもしっかり勉強しておけるといいですね。いろんな証明問題と触れる事で、対応力がついていきます。証明問題を解けるという事は、問題の本質が見えていて、しっかり解答全体を見通す力があるということです。証明問題の解答が、解答者の理解を分かりやすく教えてくれます。自分の理解を見せつけるためにも、整ったきれいな解答を作る事を意識していけるといいでしょう。

今回も最後まで読んで頂きありがとうございました。
今後も宜しくお願い致します。