久しぶりの高校数学の振り返り投稿になります。
今月中に青チャートを数Ⅲまで全て記事を書き上げます。
とりあえず今回は、「2_1_式と証明」を振り返っていきます。
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/1a1cd25e.24151616.1a1cd25f.d286440e/?me_id=1251035&item_id=18142213&m=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fhmvjapan%2Fcabinet%2Fa03%2F86000%2F10384570.jpg%3F_ex%3D80x80&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fhmvjapan%2Fcabinet%2Fa03%2F86000%2F10384570.jpg%3F_ex%3D128x128&s=128x128&t=picttext "[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]")
目次
- 概要
- 考察
- 2-1-1 三次式の展開と因数分解、二項定理
- 2-1-1-1 有名な三次式の展開
- 2-1-1-2 二項定理
- 2-1-1-3 多項定理
- 2-1-1-4 指数の拡張と指数法則
- 2-1-2 整式の割り算
- 2-1-2-1 整式の割り算の考え方
- 2-1-3 分数式とその計算
- 2-1-3-1 分数式の四則計算
- 2-1-4 恒等式
- 2-1-4-1 恒等式とは
- 2-1-4-2 恒等式の性質
- 2-1-4-3 恒等式であることの証明
- 2-1-5 等式の証明
- 2-1-5-1 等式の証明の基本
- 2-1-5-2 比例式の扱い
- 2-1-6 不等式の証明
- 2-1-6-1 不等式の証明の基本
- 2-1-6-2 実数の平方と不等式の関係
- 2-1-6-3 相加相乗平均
- 2-1-1 三次式の展開と因数分解、二項定理
- まとめ
概要
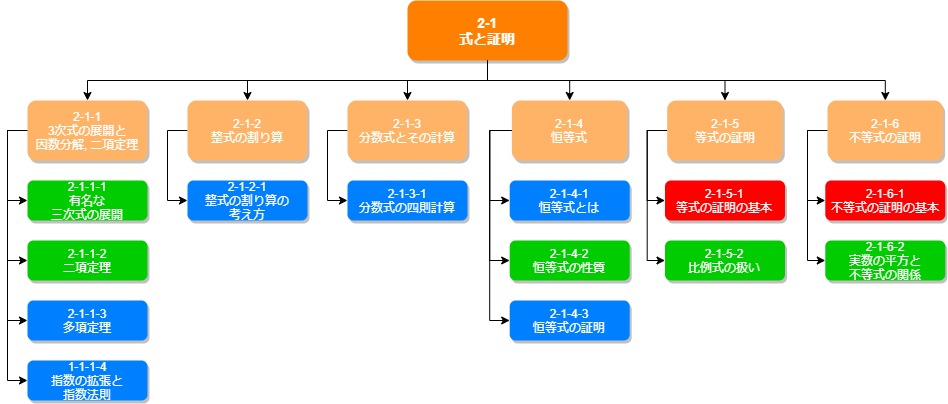
2-1 式と証明は、1-1 数と式の発展形です。「数と式」では2次式までがメインだったのに対して、ここでは3次式までを取り扱ったり、2次不等式を扱ったりしていきます。少しずつ複雑になってきますが、一つ一つ確実に抑えていきましょう。
ここの考え方は、指数対数や微積でも必ず使うことになるので、しっかり勉強しておかないといけません。
2-1-1では、3次方程式で覚えておくべき頻出の変換式と二項定理などを中心に学習します。
2-1-2では、整式の割り算を学習します。A-4 整数の性質で学習した、整数の割り算の形を覚えていれば、同じ形で表現することができます。それぞれの項が整数から整式に変わっただけです。
2-1-3では、分数式の考え方を学習します。ここも2-1-2同様、文字が整式を表すようになったというだけで、分数式の扱いは普通の分数と同じです。
2-1-4では恒等式を学習します。恒等式の考え方は慣れるまで難しいかもしれませんが、しっかり意味を理解して考えていけるようにしておきましょう。
2-1-5, 2-1-6は証明問題になります。基本的な処理の仕方を確認しておけば大抵の問題は解くことができるので問題ないでしょう。難関校レベルの難しい問題は少し演習が必要だと思うので、ここではとりあえず基本レベルの問題を解けるように学習しておけるといいでしょう。
考察
2-1-1 三次式の展開と因数分解、二項定理
2-1-1-1 有名な三次式の展開
これらは頻出の式なので、3次式の有名な展開の形として覚えておきましょう。
2-1-1-2 二項定理
二項定理は数Ⅰの分野でも学習しましたが、ここでは発展形として、コンビネーションを使った表現方法を学習しておきましょう。組み合わせの考え方もしっかり理解した上で覚えておきましょう。
(a+b)n = Σ( nCi×aibn-i )
シグマ記号の使い方はB-3 数列の分野で学習するので、そこを学習してからもう一度見直しましょう。
2-1-1-3 多項定理
多項定理とは、(a+b+c)nといったn次式を展開した時に、一般項はどのように表されるかを考えるものですが、反復試行の考え方を学習していれば難しいことはありません。こういった名前がついているんだな程度に確認しておけばいいでしょう。
(a+b+c)nを展開した時、一般項は、( n!/p!q!r! ) × apbqcrと表される。
2-1-1-4 指数の拡張と指数法則
指数の拡張は、ゼロ次式やマイナス次式をどのように考えるのか表しています。0次式は1となり。マイナス次式は逆数を考えると覚えておきましょう。
また、指数は以下のようになります。
いずれも指数関数を勉強すれば、イメージは掴むことができるでしょう。
1, aman = amn
2, (am)n = amn
3, (ab)n = anbn
2-1-2 整式の割り算
2-1-2-1 整式の割り算の考え方
整式Aを整式Bで割るという整式の割り算は、
A = QB + R （Q, Rは整式を表す）
として定式化されます。
Qが商、Rが余りを表し、Rの次数はBよりも小さくなっています。
2-1-3 分数式とその計算
2-1-3-1 分数式の四則計算
分数式の四則計算は、一般の分数と同じ形で表されます。簡単に確認しておきましょう。
1, 乗法：A/B × C/D = AC/BD
2, 除法：A/B ÷ C/D = AD/BD
3, 加減法：A/C ± B/C = ( A ± B ) / C
2-1-4 恒等式
2-1-4-1 恒等式とは
恒等式とは、変数にどんな値を入れても常に成り立つ式を表します。
0x3 + 0x2 + 0x = 0
例えば、簡単に言うと、このような式があった時、xにどんな数字を代入しても成り立つことが分かるでしょう。正しい例かどうか分かりませんが、このように変数に関係なく成立する式が恒等式です。
演習を重ねながら理解を深めていきましょう。
2-1-4-2 恒等式の性質
整式P, Qについて、
1, P=0が恒等式である時、Pの各項の係数は全て0になる
2, P=Qが恒等式である時、PとQの項について、次数が等しい項の係数は等しくなる。
これらの性質はよく使う考え方なので、迷わず使いこなせるようにしっかり確認しておきましょう。
2-1-4-3 恒等式であることの証明
「n次式の整式P, Qについて、(n+1)個の変数についてP=Qが成立する時、P=Qは恒等式であると言える」
頻出ではありませんが、頭の隅に入れておきましょう。
2-1-5 等式の証明
2-1-5-1 等式の証明の基本
等式A=Bの証明方法は、大きく三つです。
1, A, B一方を変形させて、他方を導くことで、A=Bとする
2, A, Bそれぞれを変形させてCを導くことで、A=B=Cとする
3, A-B=0を導くことで、A=Bとする。
等式の証明で迷った時は、しっかりこの原点に立ち戻ることで、式変形を進めていくことができることが多々あります。基本的なところですが、基本的なところだからこそ大切にできるといいでしょう。
2-1-5-2 比例式の扱い
比例式とは、a:b = c:d ⇔ a/b = c/dと表される式です。
比例式が出題された時は、a/b = c/d = k(定数)と考えて、a=kb, c=kdと変形するのがポイントになります。この作業を行うことで、a,b,c,dと文字が4つ存在していたところを、a,b,kの3文字に減らすことができます。
よく使う手法なので確認しておきましょう。
2-1-6 不等式の証明
2-1-6-1 不等式の証明の基本
不等式A>Bの証明方法は1つしかありません。
証明方法自体は非常に簡単ですが、実際の問題はかなり複雑になってきます。演習を重ねて、慣れていきましょう。
A-B>0を導くことで、A>Bとする
2-1-6-2 実数の平方と不等式の関係
実数の平方と不等式の間には以下の関係があります。
問題の中で使えるように確認しておきましょう。
1, a2 ≧ 0 （等号はa=0で成立）
2, a2+b2 ≧ 0 （等号はa=b=0で成立）
3, a>0, b>0の時、a2 ≧ b2 ⇔ a ≧ b
2-1-6-3 相加相乗平均
相加相乗平均は以下の式によって定式化されます。
難関校レベルの問題では頻出です。相加相乗平均を使うことを思いつかないと解けない問題が多々あるので、抵抗なく相加相乗平均を意識できるようにかみ砕いておきましょう。
a>0, b>0の時、(a+b)/2 ≧ √(ab) （等号はa=bで成立）
まとめ
今回からは数Ⅱの範囲に入っていきます。数Ⅱは非常に範囲が広く、とても大変です。そのため、多くの受験生は数ⅡBに苦手意識をもって、数学を諦めていきます。
しかし、範囲が広いので難しくて当たり前です。大切なのは、その全体像をしっかり掴んで、一つ一つ分野の理解を深めていくことです。コツコツと正しい努力を積み重ねることで、確実に得点を向上させていくことができます。頑張りましょう。
赤のラインはポイントを、黄色いマークは覚えておくべきところを表しています。まずは黄色いところをしっかりと覚えて、演習をするための基礎を固められるといいでしょう。
(a±b)(a2∓ab+b2) = a3±b3
(a±b)3 = a3±3a2b+3ab2+b3