830の数学_2_5_指数関数と対数関数

今回は「指数関数と対数関数」を振り返っていきます。
難しいと思われがちですが、理解してしまうと非常に得点しやすいところになっているので、しっかり意味を確認していきましょう。覚えることも少ないので、確実に理解したいところです。

チャート式 基礎からの数学II+B / チャート研究所 【本】 価格：2365円（税込、送料別) (2020/4/16時点)

概要

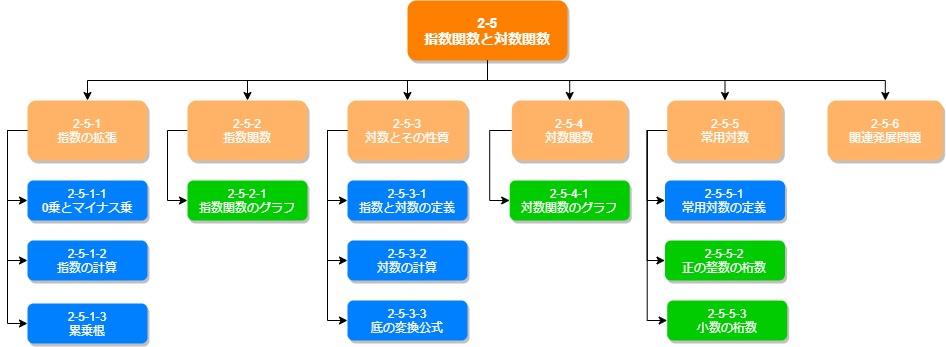
「指数関数と対数関数」は数Ⅱの中では比較的得点しやすい分野ではないかなと思います。苦手意識を持たずに取り組んでほしいです。少し計算が煩雑になる部分はありますが、丁寧に計算していければ確実に得点に結びつけられるんじゃないかなと思います。

2-5-1, 2-5-2では指数関数について学び、2-5-3, 2-5-4では対数関数を学んでいきます。指数関数と対数関数の関係もしっかり頭に入れた上で理解していけるといいでしょう。

2-5-5では常用対数です。常用対数では、正の数の桁数を答える問題と小数の桁数を答える問題の大きく2つが存在します。それぞれの考え方をしっかりと押さえておきましょう。これらを押さえておけば、常用対数の意味するところはしっかりイメージできるのではないでしょうか。

2-5-6では発展問題も準備されているので、取り組んでみましょう。

考察

2-5-1 指数の拡張

2-5-1-1 0乗とマイナス乗

0乗、マイナス乗の処理は以下のようになります。

2-5-1-2 指数の計算

指数の計算は以下のようになります。

2-5-1-3 累乗根

累乗根は指数で以下のように分数で表現されます。

2-5-2 指数関数

2-5-2-1 指数関数のグラフ

指数関数y=ka^xのグラフの描き方を確認しておきましょう。
0<a<1, 1<aでどのようにグラフが変わるのか、kが変化するとどのようにグラフが変わっていくのか、それぞれしっかり確認しておきましょう。

2-5-3 対数とその性質

2-5-3-1 指数と対数の定義

指数、対数の関係は以下のように定義されます。ここで示されるaを底と呼びます。

2-5-3-2 対数の計算

対数の計算は以下のようになります。

2-5-3-3 底の変換公式

対数の底の変換は、以下のようにすることができる。

2-5-4 対数関数

2-5-4-1 対数関数のグラフ

対数関数y=klog_axのグラフの描き方を確認しておきましょう。
0<a<1, 1<aでどのようにグラフが変わるのか、kが変化するとどのようにグラフが変わっていくのか、それぞれしっかり確認しておきましょう。

2-5-5 常用関数

2-5-5-1 常用対数の定義

底が10の対数を常用対数と言います。常用対数を用いることで、整数の桁数などについて議論ですることができます。正の数Nについて、以下のような書き換えを確認しておきましょう。

2-5-5-2 正の整数の桁数

正の整数Nの桁数は以下のように計算することができます。

2-5-5-3 小数の桁数

小数Nに初めて0出ない数字が表れる桁数は以下のように計算することができます。

2-5-6 関連発展問題

まとめ

「指数関数と対数関数」では、それぞれの計算がしっかりできれば、それほど複雑な問題は出題されません。それぞれ関数のグラフと合わせて、意味も確認して、確実に得点できるようにしておきましょう。

対数に関しては、常用対数を用いた桁数の計算という頻出の問題があるので、こちらも確認しておきましょう。